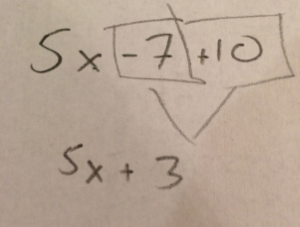Open Equations - Getting Students To Solve Equations Creatively

I ended my last blog post wishing that my students had the chance to solve equations creatively. I think I have found a structure (heavily influenced by Chapter 5 of the book Thinking Mathematically) that will give students this opportunity.

I am going to call these open equations. Here’s how they work:

I project an equation, such as a + 5 = b + 8, on the board.

I ask students to spend a few minutes finding at least three sets of values for a and b that make this equation true.

Then I give the students an additional few minutes to compare their answers and look for any patterns in the responses.

Then I lead a number talk with the whole class as we discuss possible solutions and any patterns that emerge.

I like this format for several reasons:

• The right side of the equation is an expression instead of a numerical value. This is intentional. I want students to stop thinking of the equals sign as the place where the answer goes and start thinking of it as a symbol that connects two equivalent expressions. I want kids to think “Whatever I make a and b, I need to make sure that a + 5 has the same value as b + 8."

• The fact that this is a two-variable equation gets kids away from finding the answer and towards finding some answers. I think this is an important distinction because it leads kids to look for patterns within their answers, something that students rarely do when solving a problem like 2x + 3 = 15. In this problem, students might think “Wow, it looks like a is always 3 greater than b. Why is that?" 

• This practice of finding pairs of values that make the solution true will be quite valuable when students begin learning about functions. Graphing a linear function just becomes another way of representing all the possible solutions for an equation. Which is exactly what the graph of a function is!

• In this format, the way students look at the expressions a + 5 and b + 8 is different than the way that students often look at the expression 2x + 3 in the problem 2x + 3 = 15. In the latter problem, students often view that expression as a series of steps that need to be undone. They go operation hunting in order to solve the equation without considering that 2x + 3 is an object in and of itself. I want kids to think of a + 5 and 2x + 3 as things. That’s how I view them and how I think other fluent algebraic thinkers see them as well. Fluent readers see sentences as things as well as seeing each component of a sentence on its own. Fluent writers know how they can manipulate the components of a sentence and still maintain its original meaning. I want my students to be fluent algebraic thinkers. I want them to see the forest and the trees.

I’ve given one simple equation above, but there are a lot of other examples that I think could help students with any number of math topics.

Are students simplifying their expressions incorrectly? Give them the open equation a - 7 + 10 = b and ask students why b is always 3 greater than a.

Are students having trouble combining like terms? Give them an open equation like a + a + a + a = b + b + b. Students will pretty quickly move from adding to multiplying a by 4 and b by 3. If you want, there is a bonus lesson about proportionality in this equation!

Want to explore the distributive property?  Give students the open equation 2(a + 5) = 2b + 10 and ask them to find three pairs of answers. Why are the values of a and b always the same? Could I rewrite the equation as 2(a + 5) = 2a + 10? Can any students write another open equation where a and b are always equal?

Most importantly, I think that this format becomes more successful the more frequently it is used. I use them as warm-ups and like to think of it as a slow-motion number string, but you could work through several equations in a row if the need arises.

I have many, many more ideas for how open equations can be used as a gateway to solving equations. And I will be writing a lot more about those ideas and fleshing them out online and in my classroom.

But the purpose of open equations is not to get students to be better at solving equations. The purpose of open equations is to get students to understand equations. Once they understand how equations relate two equivalent quantities, then they can build their own strategies to solve problems like 2x + 3 = 15. And when we move from informal to formal strategies, they will have a basis for understanding those formal strategies and why they work.

Let me know what you think!

Stop the Operation-Hunting

I’d like to talk about an incredibly common mistake that students make when simplifying expressions. And I’d like to talk about why I completely empathize with students and see why they must be so flabbergasted when this problem is marked wrong.

First, the mistake.

The amazing thing about this type of mistake is how insistent my students are that they have not made a mistake at all. For the most part, my students feel ill at ease when simplifying expressions, but this problem feels like sturdier ground to them. And yet it is wrong! How can this be?

I think that students’ confusion comes from a very understandable place: order of operations. When most students learn about order of operations, they learn it as a process of operation-hunting. They look for each operation in turn and then grab the number to its left and right in order to evaluate the problem. Normally, it looks something like this:

Why do you multiply 5 and 4? Because those are the numbers connected by the multiplication sign, of course! Ditto for the subtraction and addition signs.

So a couple of days or weeks later, you ask your students to simplify 5x - 7 + 10. They start their operation hunt. First they find the implied multiplication of 5 and x, but since that can’t be simplified, they move on. Then they find the subtraction sign, but since 5x and 7 aren’t like terms, they can’t be subtracted. So all they have left is addition! Grab the number on the left and right and evaluate! Simple as pie.

This is why kids are so baffled when I mark this answer wrong. It feels like a repudiation of their well-earned knowledge about the order of operations. And it is! At least, it’s a partial repudiation. It tells students that they cannot simply hop from operation to operation, excusing one’s dear Aunt Sally until the final answer has been derived. And this tension between order of operations and the fundamental properties of math is hardly addressed.

In the past, I have tried to remediate this issue by drawing boxes around the problem like so:

This doesn’t really make sense to students. First of all, since when can you put a box around part of an expression? The“- 7” doesn’t look like a valid math expression and neither does “+ 10". It's a fundamentally different way of looking at the problem than the way that I've taught them to look at 5*4 - 7 + 10. But they go along with it, I suppose, because I am big and loud and insist that this is the cool new way to think about simplifying expressions. Forget what I said in late August! It’s early September, for God’s sake!

But really, does this make any sense? Would it work with the aforementioned order of operations problem? What would you do if you saw one of your students with this work on their paper?

The curse of operation-hunting is the problem, and it must be stopped. We need students to learn the order of operations, of course, but we need to spend much more time working with kids to figure out when the order of operations can be overruled, and why.

We need kids thinking creatively about simplifying expressions. 

But how in the world do we do that?

This post is the second in a series.

The Two Types of Math Mistakes

I want to talk about the two types of math mistakes I see in my class, and why I get so excited by the first type and so depressed by the second type.

First, the mistakes. 

Problem 1: Big Horn Ranch raises 100 horses on 150 acres of pasture. Jefferson Ranch raises 75 horses on 125 acres of pasture

Problem 2:  x + x + 4 = 22

The first mistake is an error in reasoning. It's incredibly common when students are attempting a new or unfamiliar problem. Students try to apply their previous, incomplete understanding of math to a new situation and find that they don't have the tools or the understanding to get the right answer.

This mistake is exciting because it represents the beginning of a conversation. This student reasoned his way to an answer that satisfied him. All I need to do is create some dissonance within his mental model of the problem in order to get him to re-evaluate the problem. Maybe I give another more extreme set of acres and horses that are also 50 apart, such as 60 acres and 10 horses, and ask if this ranch also has the same amount of acres per horse. What about 51 acres and 1 horse? My next step depends on the student and the setting, but at least it's building on some prior understanding of the scenario.

Mistake #2 is a different animal entirely. This is not a mistake that my student reasoned her way into. This is a mistake made by someone with no understanding of equations who is desperately trying to recall some long-forgotten rule about subtracting x from both sides.

More distressingly, this is clearly a student with a lot of experience solving equations. There is no chance that this student would have tried subtracting x from 18 if she were a true novice at solving equations. And if you asked her to explain why she subtracted x from 18, she would likely have nothing meaningful to explain about preserving equality or finding the value of x. She would probably say something about "getting rid of the extra x's" and look at me terrified that I was going to ask her a follow-up question. Even her final answer of x = 17x shows that she has no consistent understanding of what a variable is and how it can be manipulated in an equation.

The second mistake depresses me because it is a mistake that I helped to create. I have taught this girl how to solve equations for weeks. And she has emerged from that experience with a worse understanding of equations than when she began. If I had given this to her on the first day of school, she probably would have at least tried to guess-and-check her way to an answer. And that would have been so much better! At least that would show that she understands the purpose of the exercise.

But no. Somewhere along the way, I helped to break something inside her head. I pushed her up the ladder of abstraction too quickly, and now she's swinging in the breeze. And fixing that issue becomes a twofold challenge. First she must unlearn before she can even begin to learn.

Almost all the mistakes the students make when solving equations are this second type of mistake. And that's something I'm going to try to change.

This post is the first in a series.