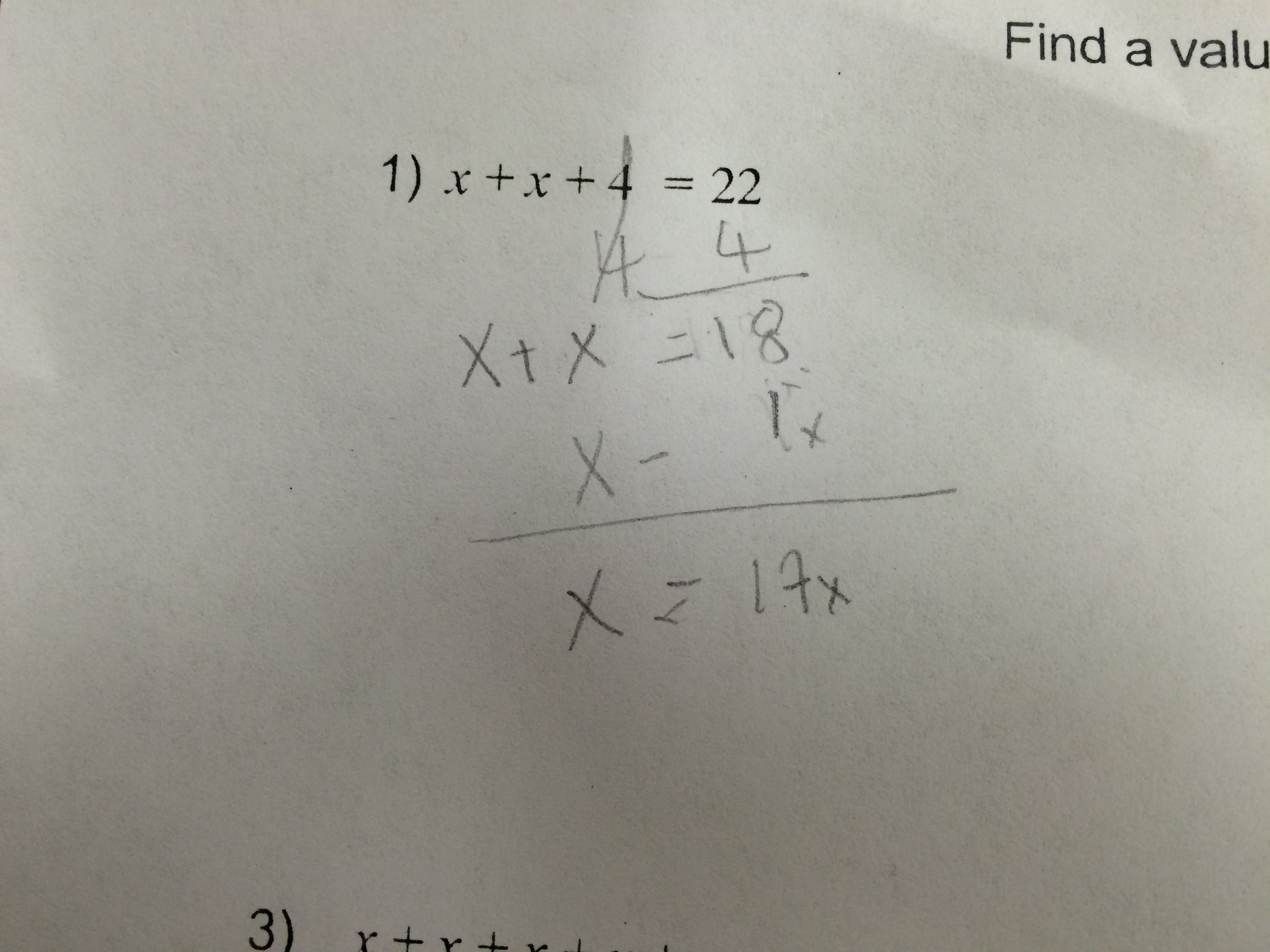I want to talk about the two types of math mistakes I see in my class, and why I get so excited by the first type and so depressed by the second type.
First, the mistakes.
Problem 1: Big Horn Ranch raises 100 horses on 150 acres of pasture. Jefferson Ranch raises 75 horses on 125 acres of pasture
Problem 2: x + x + 4 = 22
The first mistake is an error in reasoning. It's incredibly common when students are attempting a new or unfamiliar problem. Students try to apply their previous, incomplete understanding of math to a new situation and find that they don't have the tools or the understanding to get the right answer.
This mistake is exciting because it represents the beginning of a conversation. This student reasoned his way to an answer that satisfied him. All I need to do is create some dissonance within his mental model of the problem in order to get him to re-evaluate the problem. Maybe I give another more extreme set of acres and horses that are also 50 apart, such as 60 acres and 10 horses, and ask if this ranch also has the same amount of acres per horse. What about 51 acres and 1 horse? My next step depends on the student and the setting, but at least it's building on some prior understanding of the scenario.
Mistake #2 is a different animal entirely. This is not a mistake that my student reasoned her way into. This is a mistake made by someone with no understanding of equations who is desperately trying to recall some long-forgotten rule about subtracting x from both sides.
More distressingly, this is clearly a student with a lot of experience solving equations. There is no chance that this student would have tried subtracting x from 18 if she were a true novice at solving equations. And if you asked her to explain why she subtracted x from 18, she would likely have nothing meaningful to explain about preserving equality or finding the value of x. She would probably say something about "getting rid of the extra x's" and look at me terrified that I was going to ask her a follow-up question. Even her final answer of x = 17x shows that she has no consistent understanding of what a variable is and how it can be manipulated in an equation.
The second mistake depresses me because it is a mistake that I helped to create. I have taught this girl how to solve equations for weeks. And she has emerged from that experience with a worse understanding of equations than when she began. If I had given this to her on the first day of school, she probably would have at least tried to guess-and-check her way to an answer. And that would have been so much better! At least that would show that she understands the purpose of the exercise.
But no. Somewhere along the way, I helped to break something inside her head. I pushed her up the ladder of abstraction too quickly, and now she's swinging in the breeze. And fixing that issue becomes a twofold challenge. First she must unlearn before she can even begin to learn.
Almost all the mistakes the students make when solving equations are this second type of mistake. And that's something I'm going to try to change.
This post is the first in a series.