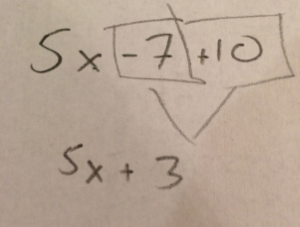I’d like to talk about an incredibly common mistake that students make when simplifying expressions. And I’d like to talk about why I completely empathize with students and see why they must be so flabbergasted when this problem is marked wrong.
First, the mistake.
The amazing thing about this type of mistake is how insistent my students are that they have not made a mistake at all. For the most part, my students feel ill at ease when simplifying expressions, but this problem feels like sturdier ground to them. And yet it is wrong! How can this be?
I think that students’ confusion comes from a very understandable place: order of operations. When most students learn about order of operations, they learn it as a process of operation-hunting. They look for each operation in turn and then grab the number to its left and right in order to evaluate the problem. Normally, it looks something like this:
Why do you multiply 5 and 4? Because those are the numbers connected by the multiplication sign, of course! Ditto for the subtraction and addition signs.
So a couple of days or weeks later, you ask your students to simplify 5x - 7 + 10. They start their operation hunt. First they find the implied multiplication of 5 and x, but since that can’t be simplified, they move on. Then they find the subtraction sign, but since 5x and 7 aren’t like terms, they can’t be subtracted. So all they have left is addition! Grab the number on the left and right and evaluate! Simple as pie.
This is why kids are so baffled when I mark this answer wrong. It feels like a repudiation of their well-earned knowledge about the order of operations. And it is! At least, it’s a partial repudiation. It tells students that they cannot simply hop from operation to operation, excusing one’s dear Aunt Sally until the final answer has been derived. And this tension between order of operations and the fundamental properties of math is hardly addressed.
In the past, I have tried to remediate this issue by drawing boxes around the problem like so:
This doesn’t really make sense to students. First of all, since when can you put a box around part of an expression? The“- 7” doesn’t look like a valid math expression and neither does “+ 10". It's a fundamentally different way of looking at the problem than the way that I've taught them to look at 5*4 - 7 + 10. But they go along with it, I suppose, because I am big and loud and insist that this is the cool new way to think about simplifying expressions. Forget what I said in late August! It’s early September, for God’s sake!
But really, does this make any sense? Would it work with the aforementioned order of operations problem? What would you do if you saw one of your students with this work on their paper?
The curse of operation-hunting is the problem, and it must be stopped. We need students to learn the order of operations, of course, but we need to spend much more time working with kids to figure out when the order of operations can be overruled, and why.
We need kids thinking creatively about simplifying expressions.
But how in the world do we do that?
This post is the second in a series.