I am contributing to Tina Cardone's Day in the Life series this year. I'll be writing about the 12th of each month.
Today was a little rough.
Some context: My wife spent the weekend at a wedding in Philadelphia, so I was home with my 4 year old son and 1.5 year old daughter. I knew this on Friday and tried to get everything ready for Monday ahead of time, but it felt rushed. So instead of refreshing my memory and refining my plans on Sunday night, I fell asleep
Then this morning I had to get both kids fed, dressed and out the door by 7am (wife still not home) so that I could get to school by 7:50. My first period came in at 8:05. So needless to say, I wasn't in the groove yet when they arrived.
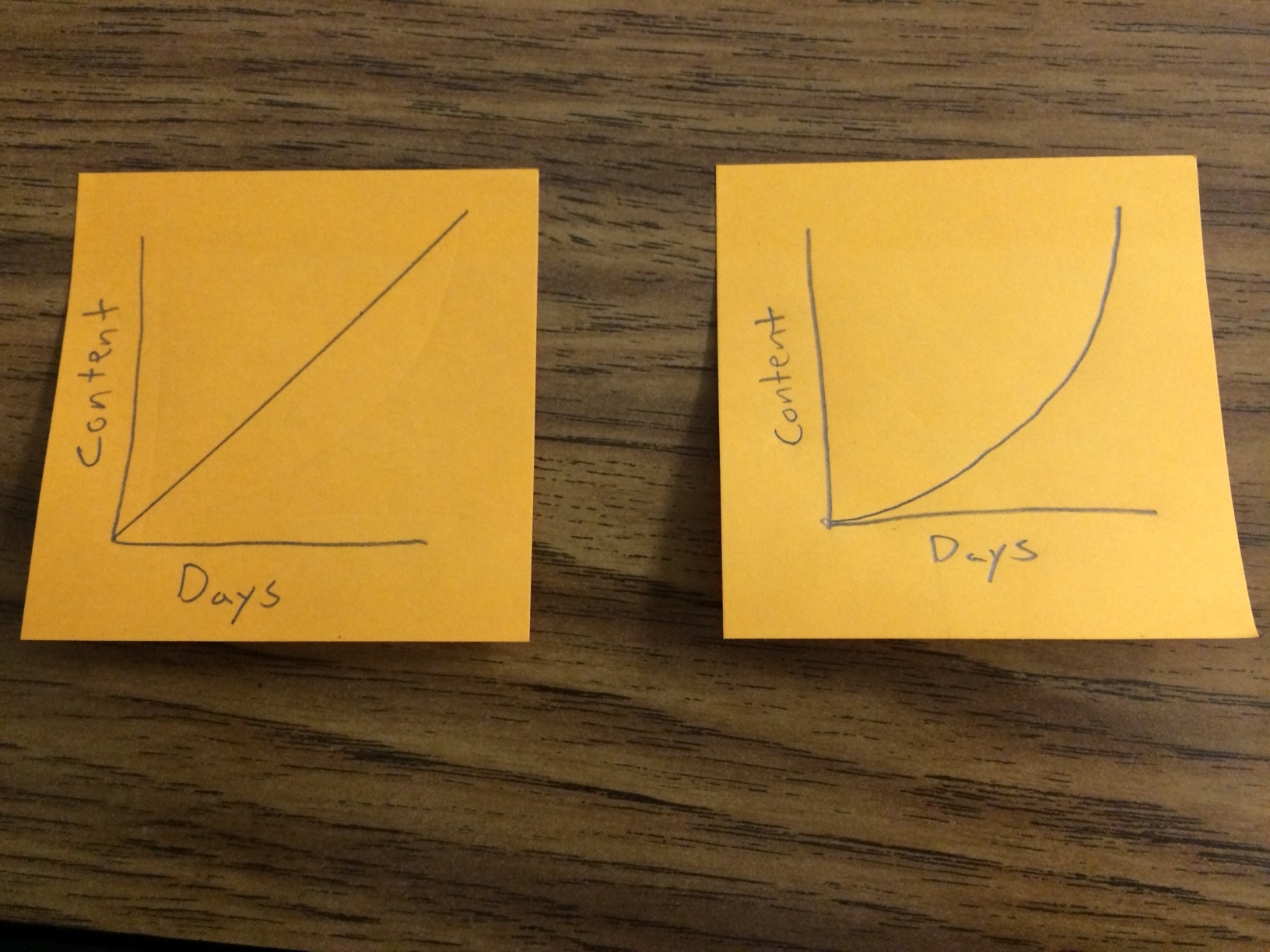
My Pre-Algebra lesson today is an introduction to the Pythagorean Theorem. In general, I like to start my units slowly. I'd rather make sure everyone is beginning from a place of comfort and then ramp up the intensity towards the end of the unit. This is not how I've always taught, but rather an approach I've developed over time.
Left:How I used to introduce new content. Right: How I introduce new content now.
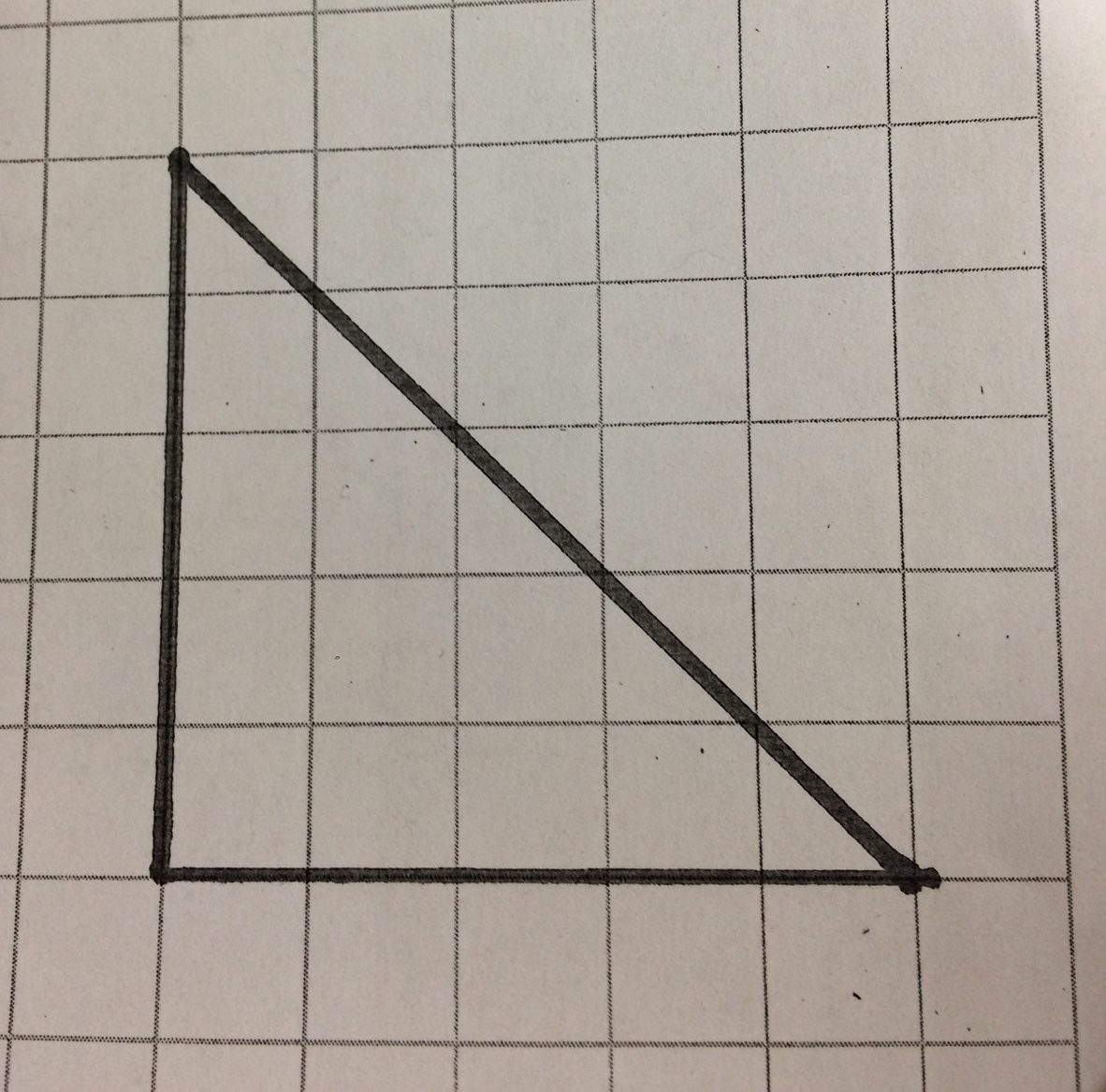
So I'm not going to use the phrases "Pythagorean Theorem" on day 1. Instead, I hand everyone a slip of paper with this triangle on it.
I ask them to brainstorm everything they know about the triangle in groups. As I walk around I start to hear encouraging words like "perpendicular" and "isosceles." My students, for some reason, are particularly behind in geometry. I don't know if it's a matter of emphasis district-wide or some other reason, but I find that there is no such thing as "too obvious" in 8th grade geometry.
After collecting some ideas on the board, I have something like this:
- Right angle
- Isosceles (two sides the same, one different)
- The short sides are each 5 blocks long
- The area is 12.5 blocks
Now I ask the motivating question for the entire day (and unit, really):
How long is the longest side?
This is the point at which my planning really fell off the rails. I expected my students to notice immediately that the longest side was longer than 5 blocks, but this turned out to be very controversial. You see, the long side does cut through 5 blocks, so some kids thought it was the same length as the others.
I ended up getting a bunch of rulers and asking the students to measure all 3 sides with the centimeter side. We got 6.5, 6.5, and 9 inches as the measurements.
Then one student said "The long side is 7."
Pardon?
"I used my ruler to see how many blocks long 9cm was, and it's 7 blocks. So the short sides are 5 and the long side is 7."
Holy crap - she's right! Or at least, the long side is VERY close to 7. In fact, we are going to prove that very thing today! And she discovered it on her own using a totally different method!
I had lightning in a bottle, but honestly, I had no idea what to do with it.
Then I looked around the room and saw how my students' engagement level was dipping. So I asked them "Can someone explain E's strategy for finding the length of the long side?"
Nobody could. So I asked E to explain herself again.
I ask again "Can someone explain E's strategy?" Still nothing.
I realize that I have done a bad job of implementing a very important element of classroom culture: the idea that students need to listen to each other.
So I start calling on students at random, asking them whether they can explain E's method. Three students in a row can't explain it, even after E repeats herself to each of those students. Finally the fourth student explains her strategy.
I am running out of time and we aren't even close to done with this lesson. So I wrap up with a crappy little lecture about the importance of listening that I am sure sailed right out of their heads the second the bell rang.
Fortunately, I had a free period to reflect on this experience.
Revised lesson plan
In my second and third Pre-Algebra classes, I explicitly pointed out this method of measurement, but complained about its imprecision. "This is the best we can do? Get out a ruler, measure the line, and then measure some blocks to estimate how long the line is? There's got to be a better way!"
That is a common refrain in my class. I do the whole infomercial voice and everything.
So then I hand out this sheet of paper, where the triangle has a square coming off its hypotenuse. I ask students to draw and shade in squares for the two legs.
We talk about how the small squares have an area of 25, which makes sense because the square root of 25 is 5, which matches the side lengths. So then if we knew the area of the big square, we could take the square root to find the length of the hypotenuse!
Then I get the kids to count the squares inside the big square. Most kids come up with something around 50, which leads to a side length of roughly 7.07. Pretty good thinking, E!
I wrap up class by saying "So that's how you find the long side of a triangle. You draw it on grid paper, then make a square from the long side, then count the area of that square, then take the square root of that area to find the length. Unless... there's a better way."
We'll be cutting out the small squares and fitting them into the big square like puzzle pieces tomorrow.
Reflection Questions:
1) Teachers make a lot of decisions throughout the day. Sometimes we make so many it feels overwhelming. When you think about today, what is a decision/teacher move you made that you are proud of? What is one you are worried wasn’t ideal?
I am proud that I was able to incorporate E's idea into my subsequent lessons, even if her class didn't get that same experience. I'll be sure to bring them into the fold tomorrow.
My worst decision was not making 10 minutes to review my lesson at some point on Sunday night or Monday morning before I taught it. I need a fresh look at a lesson within 24 hours of when I teach it. Planning a lesson on Friday for Monday is fine, but only if I review it quickly on Sunday or Monday.
2) Every person’s life is full of highs and lows. Share with us some of what that is like for a teacher. What are you looking forward to? What has been a challenge for you lately?
My challenge right now is managing all my responsibilities in school while also pursuing career goals outside of my classroom and being the primary parent. Here are my yearlong goals aside from "be a good 8th grade math teacher"
- Pilot a standards-based grading system with my 8th grade math colleagues
- Complete at least 2 components for National Board Certification
- Begin research on how kids comprehend expressions and equations for my Heinemann Fellowship
- Refine my integer unit before I present it at ACTM in November, and then refine it further and create a website to house the unit as a whole
- Brainstorm a daylong and a weeklong early math camp in the style of Math on a Stick and Talking Math With Your Kids
- Tutor a former student who is struggling in high school geometry.
- Keep my blog interesting, including with these posts
It's a lot. Something's probably going to fall by the wayside, and I don't know what.
3) We are reminded constantly of how relational teaching is. As teachers we work to build relationships with our coworkers and students. Describe a relational moment you had with someone recently.
I have a student who started the year with a pretty oppositional attitude to her teachers. On top of that, she has significant conceptual gaps in her math background. But she is a critical thinker and can make connections on her own when given enough support.
So I have been giving her praise whenever it felt authentic to me, and meeting with her some one-on-one to give her some of the foundation she needs to succeed in my class. She is slowly warming up to me.
4) Teachers are always working on improving, and often have specific goals for things to work on throughout a year. What have you been doing to work toward your goal? How do you feel you are doing?
I am still reading a lot. I have been working through some of the Transition to Algebra resources, which I really enjoy, and reading Connecting Arithmetic to Algebra by Russell, Schifter and Bastable. I will need to make a pre-assessment for expressions and equations by next month's post.
5) What else happened this month that you would like to share?
I am co-planning a lot with my colleagues, and I LOVE it. I love when I make a lesson that succeeds in my coworkers' classes, and I love using a lesson found or developed by a colleague that connects with my students. If I weren't coplanning, I wouldn't have even found the lesson that I screwed up today! But I am convinced it's the best way to introduce the Pythagorean Theorem that I've found.