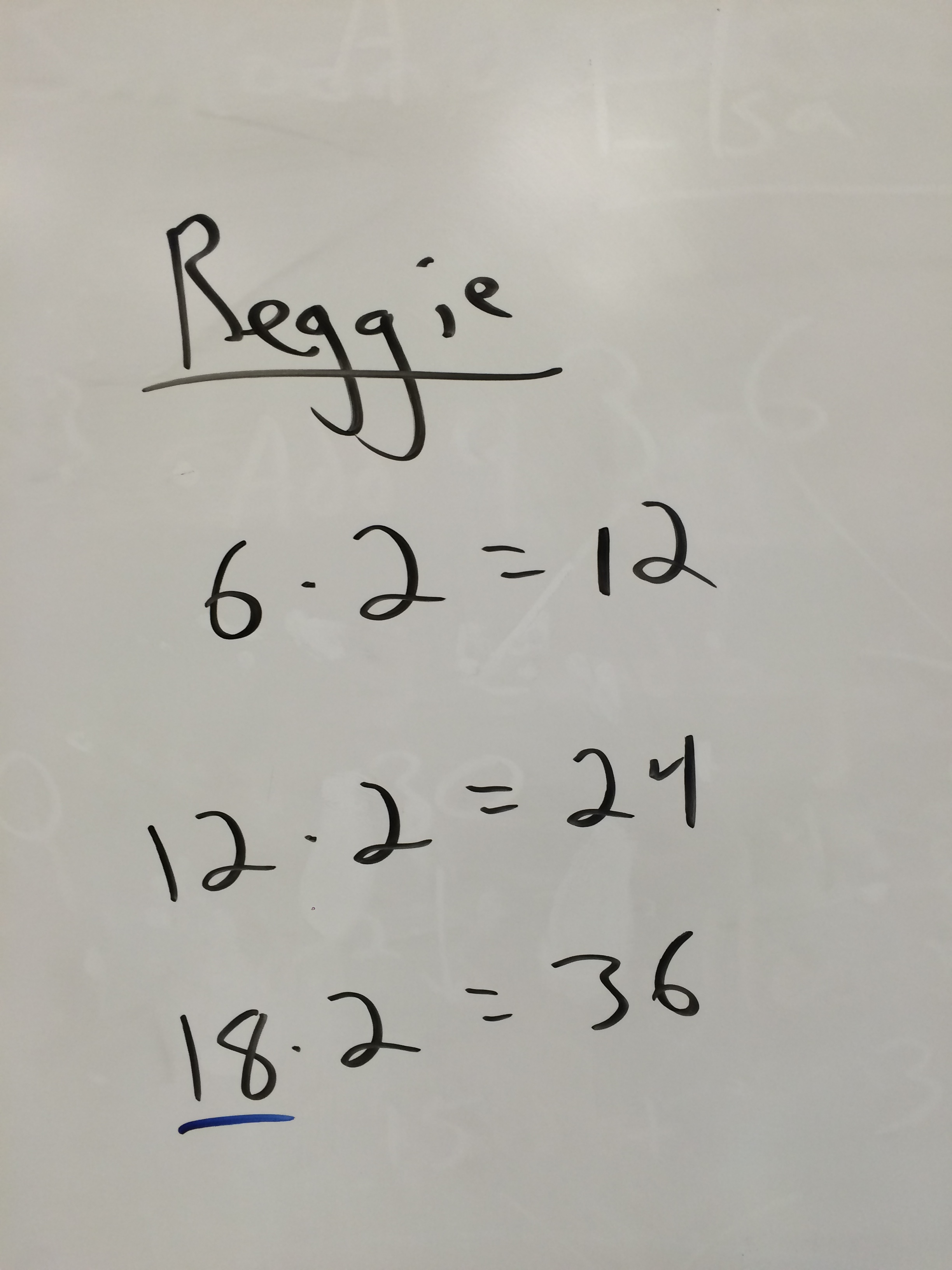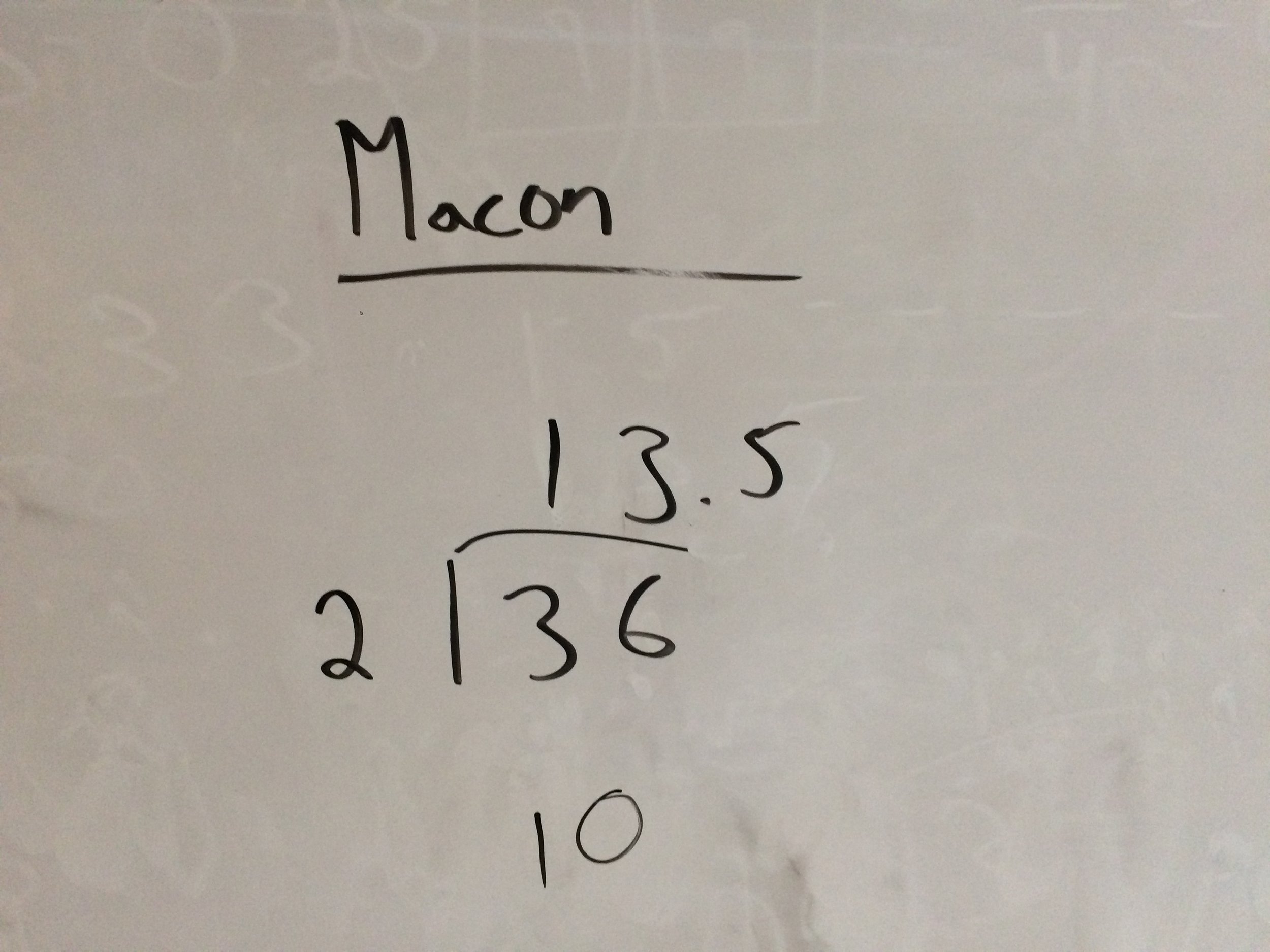In my last post, I wrote about my big-picture thoughts on Number Talks. Here's a post about the nitty-gritty.
Today in Pre-Algebra we are reviewing how to convert from fractions to decimals. I have this worksheet for all the fractions from halves to tenths. To solve this whole sheet, students will need to do some long division, so I chose a number talk that might bring up long division naturally as a strategy.
My Number Talk for today was:
Find half of 36
At the beginning of the day, I anticipate the following strategies:
- Use long division (the traditional algorithm)
- Break 36 into 30 and 6, take half of each and add the halves back together to get 18
- 6*6 is 36, so 6*3 is 18. (Not certain, but possibly
- Who knows? I'm excited to see what they come up with
Here's how it went:
A Period
Billy started us off with long division, the traditional algorithm. I'm glad he brought it up and glad to get it out of the way!
Theo said "I added a 0 and got 360. I know 360 degrees is a full circle, so 180 is a half circle. Then I took away the 0 and got 18." This was unexpected but awesome! I asked for clarification from the class as to what we are doing mathematically when we "add or take away a zero" and talked about how we are multiplying or dividing by ten.
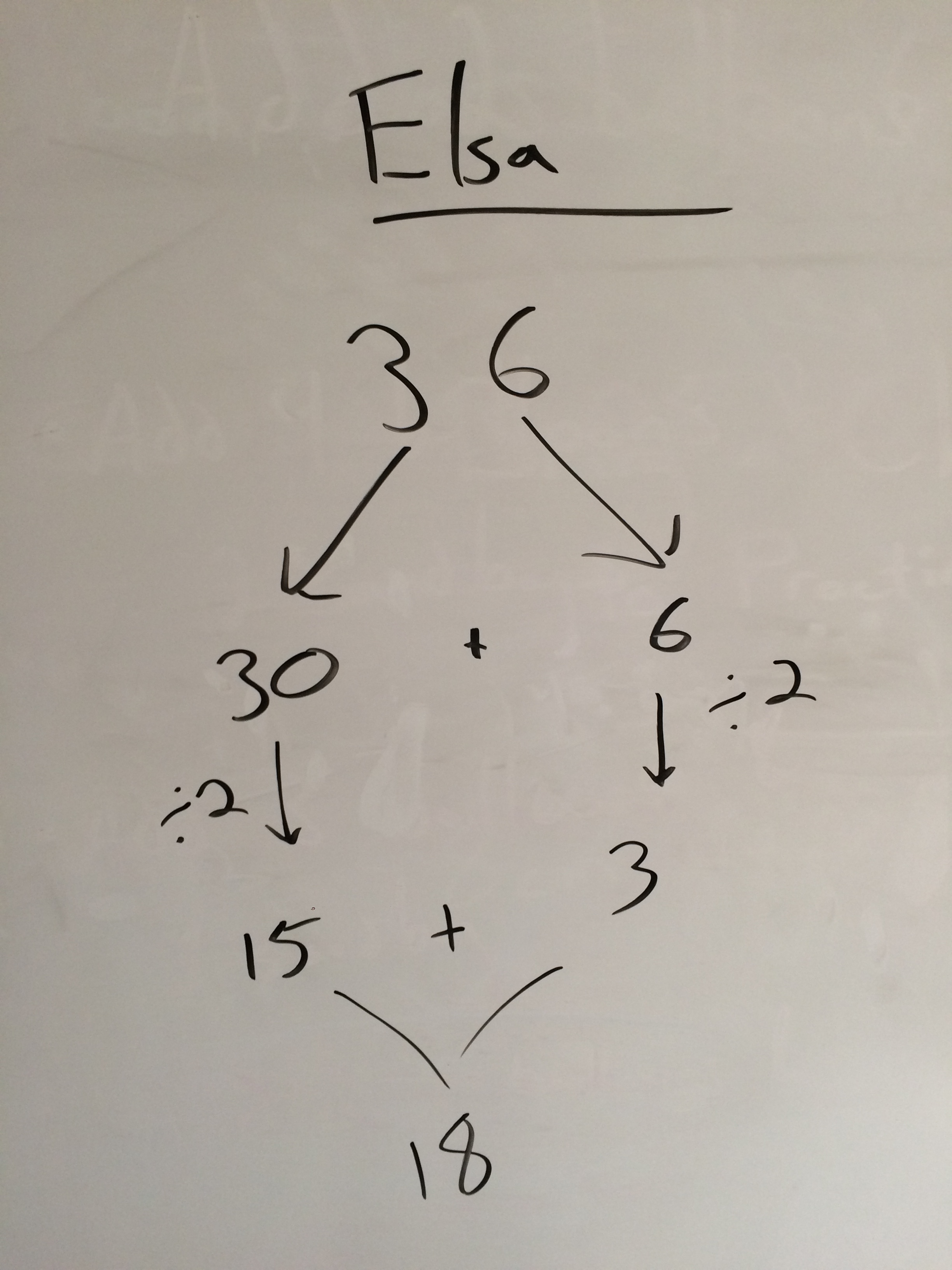
Elsa broke up 36 into 30 and 6 and found half of each, just as I anticipated. I reminded my students of the name for this strategy: decomposing 36. I like that term because it sounds gross and is memorable for that reason.
Billy said you could count by 2's until you got to 36. I wrote it down but kind of brushed it off. In retrospect, I should have dug deeper. Why does this strategy work? Why don't we count be 3s or 4s? If we did count by 3s, what would that find for us? What a missed opportunity!
Instead, I asked everyone to try Elsa's strategy on the number 74. I got a kid to explain it, and we realized that he not only decomposed 74 into 70+4, he then decomposed 70 into 60+10! So we had a double decomposition.
B Period
Ok, these guys rocked it. I had a total of 8 strategies for solving this problem!
Karina said that 3/2 = 1.5 but she knew it was really 15, so I made another student explain that part. Anna Marie used a building-up strategy to find what added to itself to equal 30 and then 6. Above, you can see where I pointed out that both of them had decomposed 36 in the process of solving their problem.
Elizabeth Rae used a similar building-up strategy to Anna Marie, but with a twist. She said "I know 15+15 is 30, and I know that 8+8=16, so I figured out that 18+18=36" I asked her to expand on that, and she said she was using the units place to figure out that 8 and 8 make a number that ends in 6, and 18 is close to 15, so it made the most sense as an answer.
Landon started with 15 as well, but multiplied by 2 instead of adding it to itself. Then he guessed and checked until he found 18.
Jackson decomposed 36 into 20 and 16 instead of 30 and 6! What a great moment! I asked the question "So can we just decompose 36 into any pair of numbers?" and a kid said "As long as they add to 36, it should work." We will definitely need to revisit this in the future.
Reggie found a pattern with 6. 6*2 is 12, and when he added 6 to the first factor and tried 12*2 he got 24, so he added another 6 and tried 18*2 to get 36. I'm still not sure how he stumbled on this idea, but it's cool! I hope he brings it up again in the future.
Jeremy decided to divide 36 by 4, since he knew that math fact. The he multiplied than answer, 9, by 2 to get 18. I asked another student to explain why this work, and I used a visual model (at the top of the picture) to solidify the explanation.
Kayla used the traditional algorithm! Finally!
C Period
This period we had our first controversy! One student got 13.5 and another got 18. All last week, we had controversy every day, so I was actualy surprised that we hadn't had disagreement in A or B period. I always get excited when a student voices a wrong answer because they might be brave enough to share their thought process and explain their mistake.
Anna Lane decomposed the problem in the way I anticipated, into 30 and 6. Haley used the traditional algorithm.
Grant did the strategy I was anticipating but unsure of, where he knew that 6*6 is 36, so 3*6 is 18. I asked him "Why not cut both numbers in half?" And he said "that wouldn't work." And I said "why?" and it got a little confused but eventually someone said "because 6*6 means you are counting six 6s, so Grant is only counting three 6s. So that's half"
After Haley did the traditional algorithm, Macon said "I see what I did wrong. I did long division, and I knew that 2 goes into 3 once and 2 goes into 6 three times. So I got 13. THen I knew I had a remainder of 1 from the 3/2, so I brought down a zero and did 10/2 and got 5, which I added at the end as 0.5. But I needed to bring down the 6 and do 16/2"
I then pointed out that his idea was almost right! He divided 30 by 2, not 3, so that 0.5 should be in the units place, where it would add with 3 to get 8. Then he would have gotten 18. This is where I wish I had my Great Mistakes board up so I could give the class a point for Macon's great mistake.
What I Learned Today
- I can anticipate the most common strategies, but some (like Theo's or Reggie's or Jeremy's) will be totally out of left field and surprise me
- Until this year, I can't think of a single time I've had 8 students share 8 different ways to solve a single problem. B Period was on fire. And we built another bit of classroom culture that the more ideas, the better.
- Macon is brave.
- I need to pull back my participation. I did a couple of moves where I said "someone else explain that to me" but in writing this blog, I realize how many times I added something that I didn't need to add.
- I like the idea of "Try Elsa's strategy on a new problem" as a good way to extend the conversation if there aren't a ton of different strategies.
- The same kids keep sharing. I think I am going to grab a couple of shy kids on Monday and say "I would love for you to share one method in our Number Talks this week. Raise your hand on a day when you feel comfortable sharing"
- In a month or so, when I introduce the distributive property, these kids are going to roll their eyes at how obvious it is. I think I will slowly formalize my notation until I write these problems in a way that looks more and more like the distributive property.