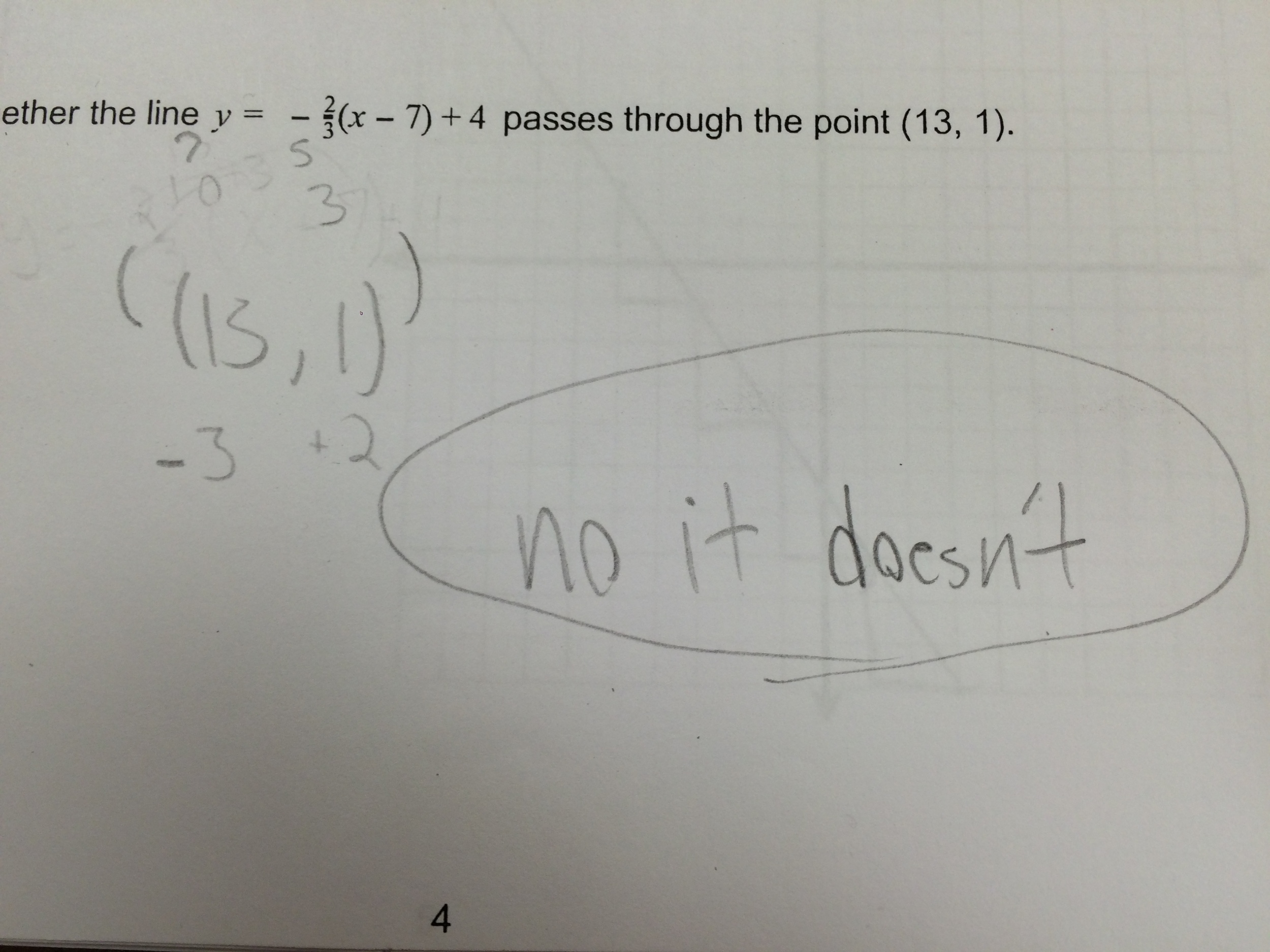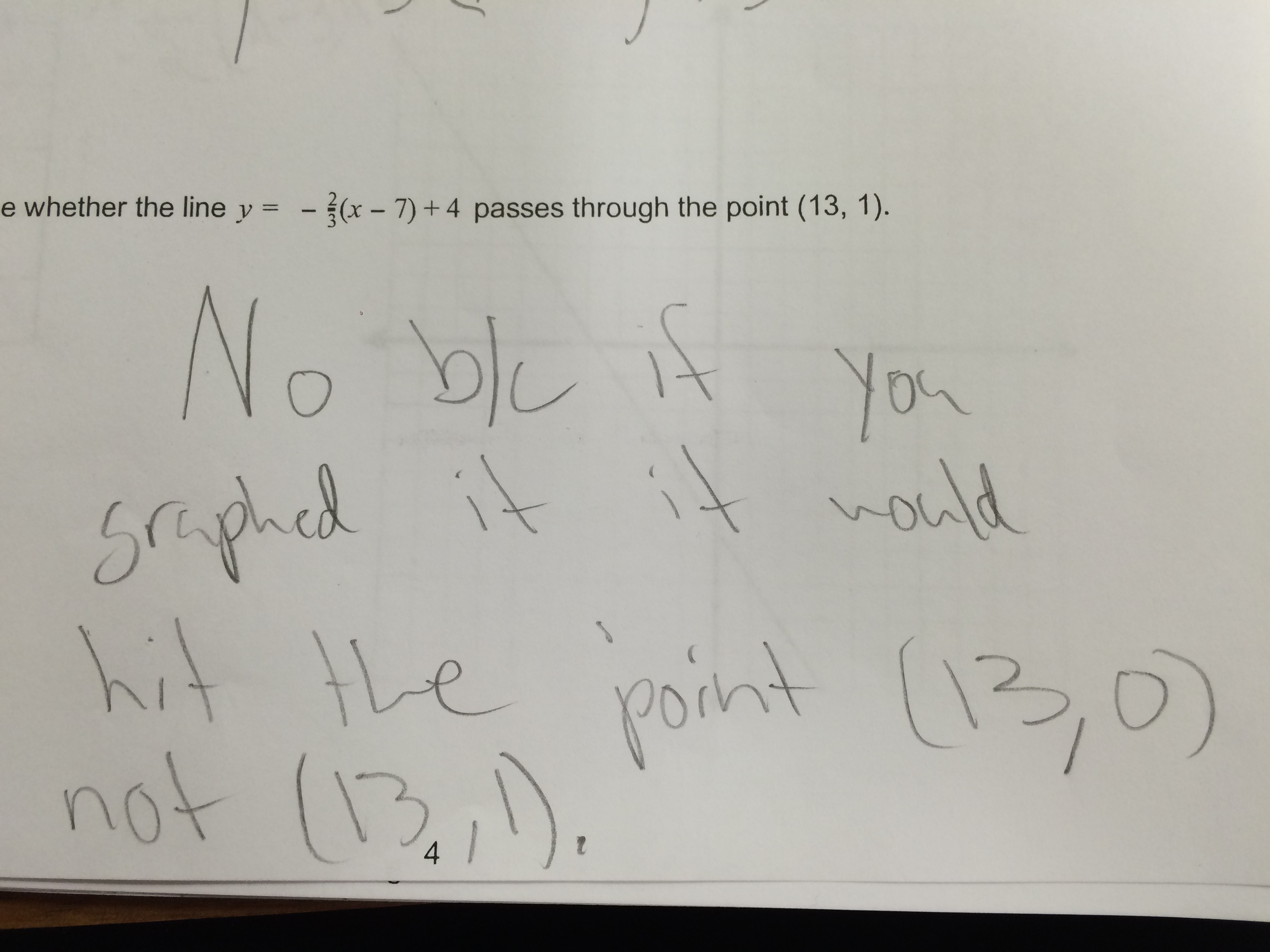My Algebra 1 students surprised me. I typically hate grading final exams, but as I was grading my students' exams I noticed something that got me legitimately excited! I was actually, enjoying the process of seeing each new student's work.
Specifically, I wanted to see how they solved problem #16.
When I wrote the question, I had anticipated that students would use a couple of different strategies. What I didn't know was that my 25 students would use a combined seven correct solution strategies to solve this problem.
Here they are, starting with the ones I anticipated.
Eight students started at (7,4) and used the slope to fill out a table or list of points until they reached the point (13,0).
Six students substituted in 13 for x and solved for y.
Four students substituted in 13 for x and 1 for y and got an impossible solution.
Now we get to my favorites:
One student, W, started at (13,1) and worked backwards up to (7,5) to determine that (7,4) was not on the same line.
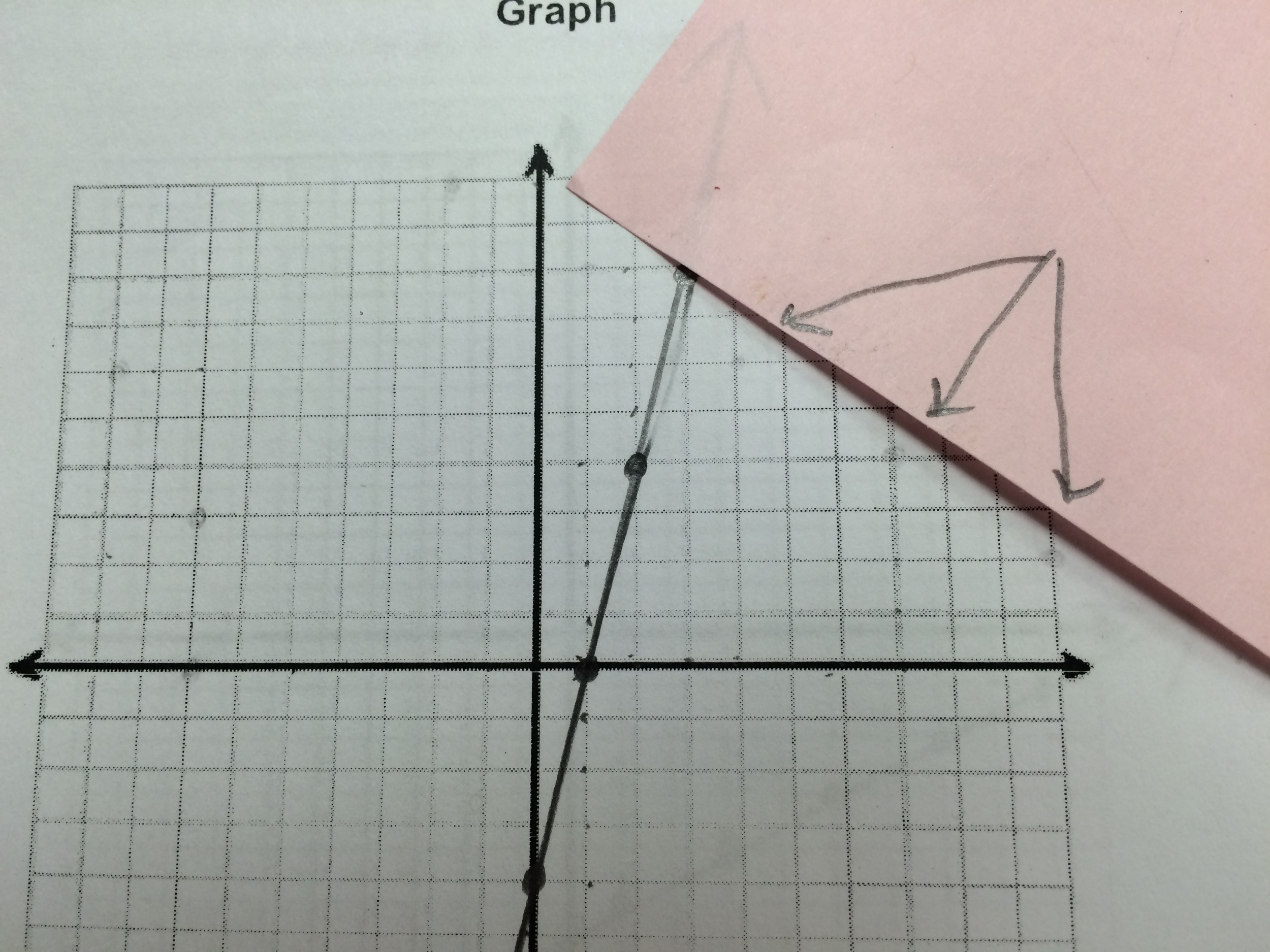
One student, K, used a coordinate plane from another page to graph the line and then wrote his justification down. He erased the points, but I found them, very faintly, on the next page.
Clever girl... (Well, he's a boy, but still)
One student, E, found the y-intercept of (0, 8 2/3) and then made a table of values from that point until he was satisfied that the line never intersected (13,1).
And my absolute favorite, the most elegant of all the solutions: One student, M, found the slope between (7,4) and (13,1) and saw that it was different from the slope of the line. QED.
Way to go, M!
(Side note: Three students got the problem wrong. Two of them substituted the y coordinate in for x, and the last student mixed up her slope and used -3/2 instead of -2/3)
I want to be clear as to why I am so thrilled. It is not because Problem 16 is some deep, challenging math problem. It's pretty straightforward and simply requires an understanding of point-slope form. It's easy to teach kids a procedure to solve it.
But I'm proud because I never explicitly taught a procedure for solving this problem. Instead, I gave a similar problem to my students in class, let them work on it in groups, and shared some of my students' various solution strategies. There was never a moment where I said "Ok, from now on always make sure to substitute this point into this equation to determine whether that point lies on the line described by the equation."
To be honest, I really didn't know at the time whether I was doing the right thing. Sure, everyone got the problem right in class (in groups, with support), but without a single procedure or mnemonic, would they be able to do it again weeks or months later?
The answer, I'm comfortable saying, is yes. My students retained the concept behind the problem. Different students chose strategies that worked best for them. Sure, E did a bunch of extra work when he found the y-intercept and made a table of values. But he used the method that made sense to him. He stopped trying to recall a set of steps and instead said "What can I find out from this information, and how can I use it to solve the problem?" M used the same approach and came up with a strategy that I had never seen until I was grading her exam. Her strategy is so elegant I can't believe I never got the chance to show it off in class!
To be honest, that's why I wrote this post. I want to brag on M. But really, I want to brag on all my students. Other kids came up with cool strategies on other problems. Kids surprised me on a final exam. My students are acting like mathematicians, y'all. They're using their toolkit of math ideas to solve problems flexibly. I couldn't be happier.
Ok, if you've followed me down here, you can read this part. I'm still secretly scared that I'm doing it wrong. Every time I get all puffed up and start to crow, a little voice in my head starts talking about how pride comes before the fall. Because after all, E doesn't have an efficient way to solve this problem. For that matter, neither does K. So did I really teach those kids how to solve this type of problem? Duct tape can hold up a light fixture if you use enough, but that doesn't mean it's up to code.
What do you guys think? Should I be proud? How can I keep improving so I reach those students who found creative-but-inelegant solutions? What about the three who missed the question - what do I do about them?