Sometimes I read about a great lesson or idea, but I am not sure how the teacher strings all these ideas together. So I’m going to blog about an entire week of teaching and explain how I tried to meld together several different types of lessons.
Weekly Goals:
My goals are for students to meet the Common Core standards shown below:
Use rational approximations of irrational numbers to compare the size of irrational numbers, locate them approximately on a number line diagram, and estimate the value of expressions (e.g., π2). For example, by truncating the decimal expansion of √2, show that √2 is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.
Know that numbers that are not rational are called irrational. Understand informally that every number has a decimal expansion; for rational numbers show that the decimal expansion repeats eventually, and convert a decimal expansion which repeats eventually into a rational number.
Explain a proof of the Pythagorean Theorem and its converse.
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
That’s a whole lot for one week! To be fair, there is a lot in these standards that I won’t be getting to. Here are my more specific learning goals:
- Find the square root of perfect squares
- Estimate the square root of other numbers
- Understand the difference b/t rational and irrational numbers, and know that many square roots of whole numbers are irrational
- Classify triangles as acute, right, or obtuse based solely on side lengths using the Pythagorean Theorem
- Find the missing side of a right triangle using the Pythagorean Theorem
Still, it’s ambitious. And to be honest, I wasn’t sure on Monday if I would even get to the missing side of a triangle. Fortunately, I have 3 days next week to use and apply the Pythagorean theorem before exam prep starts. So if I only get through classifying triangles, I’m happy.
Monday
Warm-up: Number talk about the problem 14*8.
This is the only day this week that I did a warm-up that was not connected to the material. I wish I had done more warm-ups, but unfortunately as the semester exam approaches I get nervous about running out of time. My favorite method a student used was to multiply 7*8 to get 56 twice, then add 56+56=112.
Activity:
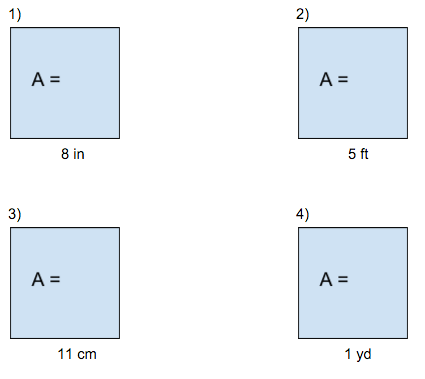
I handed out this worksheet. The front asks students to find the area of squares. I know that geometry is my students’ weakest topic in our standards, so I try to start at the very beginning. Some students didn’t know or remember how to find the area of a square. Is this shocking to me as an 8th grade teacher? Definitely. But I just walked around the room with blank graph paper. If a student couldn’t find the area of the first few squares, I asked the students to draw each square on graph paper and count the number of boxes inside each one. Every student pretty quickly realized that they could multiply the base of the square by its height.
The bottom half of the worksheet I included non-integer side lengths to prime the students for the possibility that squares can have side lengths other than whole numbers. This will come in handy on the back of the worksheet when they have to estimate square roots. In my A period class, I didn’t allow calculators, but so many students were having trouble multiplying with decimals that I let them use their calculators. After all, fluency with the multiplication algorithm isn’t the point of this lesson. Noticing patterns in square numbers is the point of the lesson.
(My favorite part of this activity was the student who got 36 instead of 1/4 as his answer to problem 6, which had a side length of 1/2 ft. I asked him how he got 36 and he said “Well, I know that half of a foot is 6 inches, so I changed the measurement to inches and got 36 square inches. Am I allowed to do that?” High fives all around.)
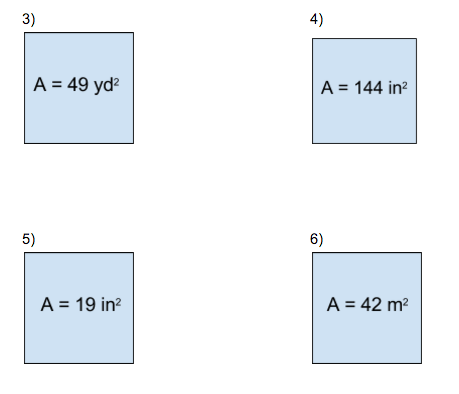
Then we moved to the back of the worksheet. On the back, I provide the area of each square and students have to find the side length. I was prepared to walk around with graph paper again so students could try to draw a square with 36 boxes in it, but nobody seemed to need it. Kids blew through the first four problems.
The bottom half of the worksheet was harder. I had kids saying “I can’t find any number that multiplies to 19,” to which I replied “What’s a side length that’s just a little too short?” Kids would usually say that 4 was too short since it gets an area of 16. Then I said “What’s a side length that’s just a bit too long?” and kids would usually answer 5.
So I would say “Hmm. 4 is too short, but 5 is too long. Weird.” and walk away. By this point in the year, the kids are used to me doing stuff like this.
(Note: Initially I used A=20 instead of 19, but I had two students who thought the best estimate was 4.5 because 4*5 =20. Then they put down a side length of 6.7 for A=42 since 6*7=42. These are both decent estimates, but for the wrong reasons. I changed problem 5 to A=19 to avoid this misconception in the future.)
Some kids came up with decent estimates for all four problems on the bottom half, while others got stuck on problem 5. Kids would show me their answers and I would ask them if they got exactly 19. Invariably they would be reeeeally close but not quite. With about ten minutes left in class I said “Competition time. The table who gets the closest answer to problem 5 wins a jolly rancher.” With this added incentive kids were furiously plugging numbers into their calculators and refining their estimates.
I would always get one or two kids in each class who knew how to use the square root button, but they only shared their solution with their table since they didn’t want to jeopardize their chance of getting a Jolly Rancher. 8th graders are teenagers, but they are still kids.
With 5 minutes to go, I collected all their estimates on the board and we tried them out as a class. Usually one table had the “right” answer of 4.358898944, which gets exactly 19 on the calculator. But I told the kids that they were ever so slightly incorrect. In fact, if they had a more precise calculator, they would see that their answer was only correct when rounded. We finished the class talking about the fact that the answer seems to keep going and going into the decimals without stopping...
Homework
Students did IXL homework on exponents, reviewing a concept from last year. I am trying to do lagging homework or “refresh” homework when I can, but I am still not good at it.
Tomorrow's Goal:
Introduce square root notation, work on estimating square roots.
Resources:
Squares and Roots Introductory Worksheet